Calculating Moments

C3 C1 L17 Calculating Moments V2

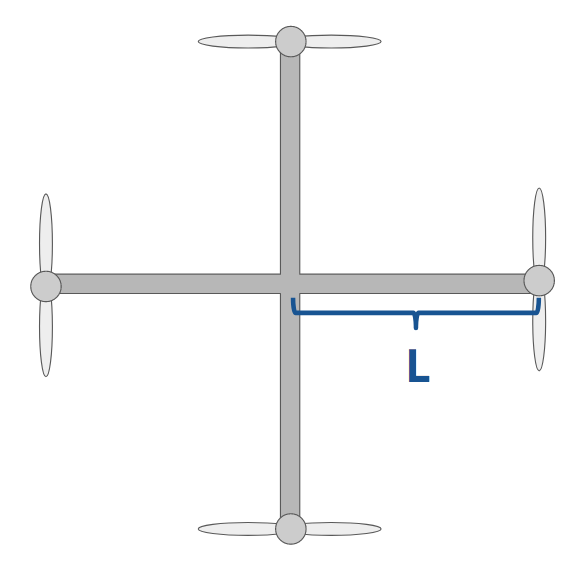
Consider the quadrotor shown above. The length of each arm is L.

How would we calculate torques If we decided to align the drone's "body" frame with the arms? If that were the case, we'd have something like the following:

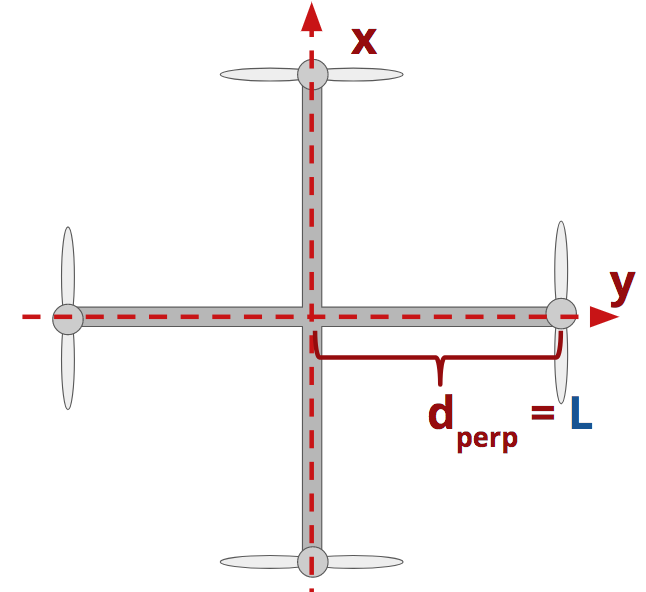
If we wanted to figure out the size of the moment about the x axis, M_x, caused by the right-most propeller, we'd do the following:

\begin{aligned} M_x &= F \times d_{\text{perp,x}} \\ M_x &= F \times L \end{aligned}

Here, the perpendicular distance to the x axis, d_{\text{perp,x}}, is exactly equal to the length of the propeller arm.

But that's not always the case! What if the body-frame coordinate system is rotated with respect to the arms? Consider the picture below.

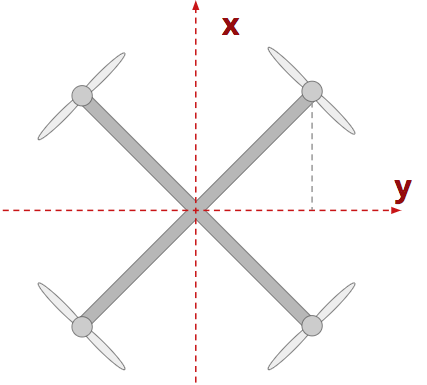
SOLUTION:

d_{\text{perp,x}} < L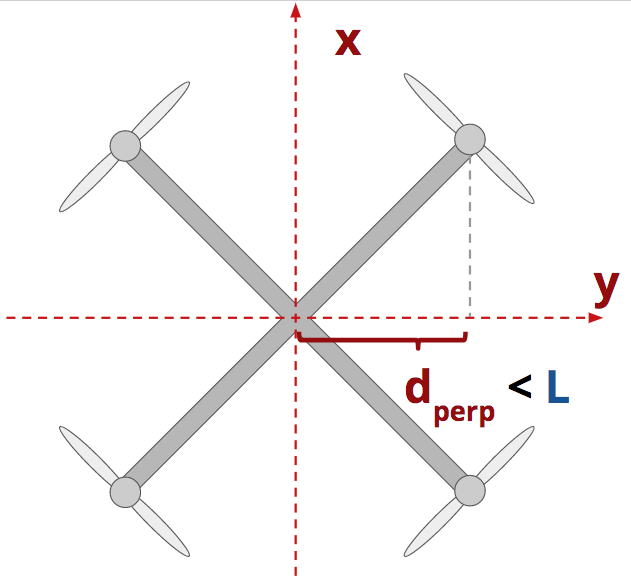

As the picture above shows, the perpendicular distance from the propeller to the x-axis is less than the length of the propeller arm.

In fact, if you look at the y-axis, the propeller arm, and the vertical line I've added to the diagram, you can start to see a right triangle emerge…

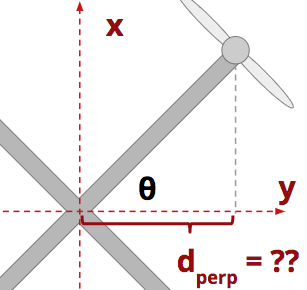
Note that the angle \theta shown in the diagram is not meant to represent the yaw of the vehicle (which we represent with \psi). It represents the angle between the rotor arm and the y-axis.

SOLUTION:

d_{\text{perp,x}} = L \cos \theta

This means that when this propeller generates a thrust F, it also generates a moment about the x axis:

M_x = F \times L \cos \theta

The coordinate system that we actually use for a quadrotor body frame has the x and y axes pointing half-way between the rotor arms. That means each arm is always at 45 degrees relative to each axis. Since \cos 45^{\circ} = \frac{1}{\sqrt{2}}, this means:

M_x = \frac{F \times L}{\sqrt{2}}

So when you see \sqrt{2} floating around in quadrotor math, this often explains why. Sometimes we will also use lower l = L / \sqrt{2} to represent perpendicular distance.